 . All the
information concerning the smoothness of
. All the
information concerning the smoothness of  can be
extracted from a table of divided differences of
can be
extracted from a table of divided differences of 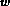 . Employing a standard
notation, see Atkinson (1988) [1], the
. Employing a standard
notation, see Atkinson (1988) [1], the 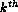 divided difference of
divided difference of 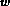 can be defined recursively as by:
can be defined recursively as by:



Let us now describe the recursive ENO algorithm for determining the
optimal stencil for the smoothest reconstruction of  . All the
information concerning the smoothness of
. All the
information concerning the smoothness of  can be
extracted from a table of divided differences of
can be
extracted from a table of divided differences of 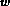 . Employing a standard
notation, see Atkinson (1988) [1], the
. Employing a standard
notation, see Atkinson (1988) [1], the 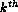 divided difference of
divided difference of 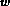 can be defined recursively as by:
can be defined recursively as by:

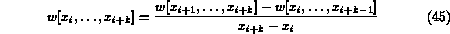
It can be shown that if the function 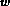 is smooth in the
interval
is smooth in the
interval 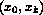 but is discontinous in
but is discontinous in 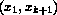 ,
then, for a
,
then, for a 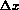 small enough :
small enough :

Hence, we can compare the relative smoothness of the function
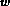 in two intervals defined by an equal number of adjacent segments by
comparing their corresponding divided differences. This fact gives us a
powerful tool to select automatically the best stencil for the smoothest
interpolation. Since all the points of the interpolating stencil must be
contigous, to specify a stencil we need only one of the two extreme points,
usually the left-most one, and the number of points in the stencil. The
smoothest-possible stencil can be built in an iterative way applying
the following algorithm:
in two intervals defined by an equal number of adjacent segments by
comparing their corresponding divided differences. This fact gives us a
powerful tool to select automatically the best stencil for the smoothest
interpolation. Since all the points of the interpolating stencil must be
contigous, to specify a stencil we need only one of the two extreme points,
usually the left-most one, and the number of points in the stencil. The
smoothest-possible stencil can be built in an iterative way applying
the following algorithm:
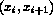 where the function is reconstructing, the first point in
the stencil will be
where the function is reconstructing, the first point in
the stencil will be 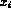 . We can represent this choice
by indicating the relative index
. We can represent this choice
by indicating the relative index 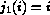 .
.
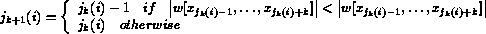
 , where
, where  is the order of
the polynomial.
is the order of
the polynomial.