


Next: The moving stencil
Up: High-Order Reconstruction Techniques
Previous: The ENO Algorithm
The reconstruction via primitive variables provides a very elegant solution
to the problem of approximating nodal values of a function once given its
cell-averages. This approach was apparently first introduced by Colella and
Woodward (1984)
[2] in their Parabolic-Piecewise Method (PPM), and
reproposed in the framework of ENO schemes by Harten et al. (1986),
[10].
The basic idea is quite simple: given a set of cell-averaged
values  , the fundamental theorem of calculus allows to
compute the exact values of the primitive function at the cell-interfaces
by an arbitrary additive constant. The primitives values can be now
interpolated in some way, providing a polynomial reconstruction of the
primitive function, and the derivative of this polynomial gives the
desidered nodal reconstruction.
Let us formalize the procedure: assume that
, the fundamental theorem of calculus allows to
compute the exact values of the primitive function at the cell-interfaces
by an arbitrary additive constant. The primitives values can be now
interpolated in some way, providing a polynomial reconstruction of the
primitive function, and the derivative of this polynomial gives the
desidered nodal reconstruction.
Let us formalize the procedure: assume that  be a set of
cell-averages of a piecewise-smooth function
be a set of
cell-averages of a piecewise-smooth function  , which is the derivative
of another (smooth) function
, which is the derivative
of another (smooth) function 

Eq. (38) is equivalent to

The discrete pointwise-values at any cell-interface position
 can be computed by applying the
following relation:
can be computed by applying the
following relation:

The lower limit  is arbitrarly fixed and any point could
actually be chosen. ENO approximations are
not affected by this choice, because a change in the lower limit only
shifts
is arbitrarly fixed and any point could
actually be chosen. ENO approximations are
not affected by this choice, because a change in the lower limit only
shifts  by a constant value, and the property defined by
Eq. (38) which the ENO algorithm effectively uses is
unaffected by a constant shift. If we assume that we are starting with
the exact cell-averages
by a constant value, and the property defined by
Eq. (38) which the ENO algorithm effectively uses is
unaffected by a constant shift. If we assume that we are starting with
the exact cell-averages  , this procedure will give us the exact
pointwise values of the primitive functions
, this procedure will give us the exact
pointwise values of the primitive functions 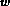 at the cell-interfaces
at the cell-interfaces
 . We can apply the interpolation to the ``smoothest''
collection of discrete values of the primitive function
. We can apply the interpolation to the ``smoothest''
collection of discrete values of the primitive function  and
obtain an ENO interpolating polynomial:
and
obtain an ENO interpolating polynomial:

We can then obtain an approximation to  which we
call
which we
call  , by differentiating
, by differentiating  :
:

Since the primitive function  is by one derivative smoother
than
is by one derivative smoother
than  , a
, a  -degree polynomial interpolation provides a
-degree polynomial interpolation provides a  -order
accurate approximation, where
-order
accurate approximation, where  . Hence, we lose one order of accuracy
because of the differentiation and we obtain:
. Hence, we lose one order of accuracy
because of the differentiation and we obtain:




Next: The moving stencil
Up: High-Order Reconstruction Techniques
Previous: The ENO Algorithm
 , the fundamental theorem of calculus allows to
compute the exact values of the primitive function at the cell-interfaces
by an arbitrary additive constant. The primitives values can be now
interpolated in some way, providing a polynomial reconstruction of the
primitive function, and the derivative of this polynomial gives the
desidered nodal reconstruction.
Let us formalize the procedure: assume that
, the fundamental theorem of calculus allows to
compute the exact values of the primitive function at the cell-interfaces
by an arbitrary additive constant. The primitives values can be now
interpolated in some way, providing a polynomial reconstruction of the
primitive function, and the derivative of this polynomial gives the
desidered nodal reconstruction.
Let us formalize the procedure: assume that  be a set of
cell-averages of a piecewise-smooth function
be a set of
cell-averages of a piecewise-smooth function  , which is the derivative
of another (smooth) function
, which is the derivative
of another (smooth) function 





 can be computed by applying the
following relation:
can be computed by applying the
following relation:

 is arbitrarly fixed and any point could
actually be chosen. ENO approximations are
not affected by this choice, because a change in the lower limit only
shifts
is arbitrarly fixed and any point could
actually be chosen. ENO approximations are
not affected by this choice, because a change in the lower limit only
shifts  , this procedure will give us the exact
pointwise values of the primitive functions
, this procedure will give us the exact
pointwise values of the primitive functions 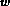 at the cell-interfaces
at the cell-interfaces
 . We can apply the interpolation to the ``smoothest''
collection of discrete values of the primitive function
. We can apply the interpolation to the ``smoothest''
collection of discrete values of the primitive function  and
obtain an ENO interpolating polynomial:
and
obtain an ENO interpolating polynomial:

 , by differentiating
, by differentiating  :
:

 -degree polynomial interpolation provides a
-degree polynomial interpolation provides a  -order
accurate approximation, where
-order
accurate approximation, where  . Hence, we lose one order of accuracy
because of the differentiation and we obtain:
. Hence, we lose one order of accuracy
because of the differentiation and we obtain:
